
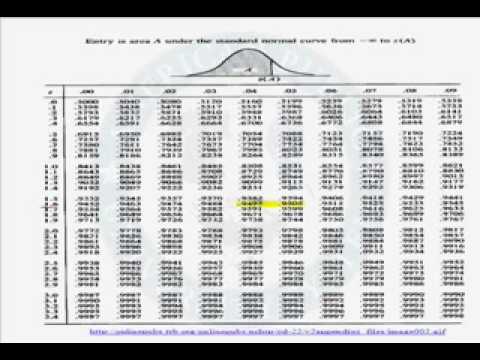
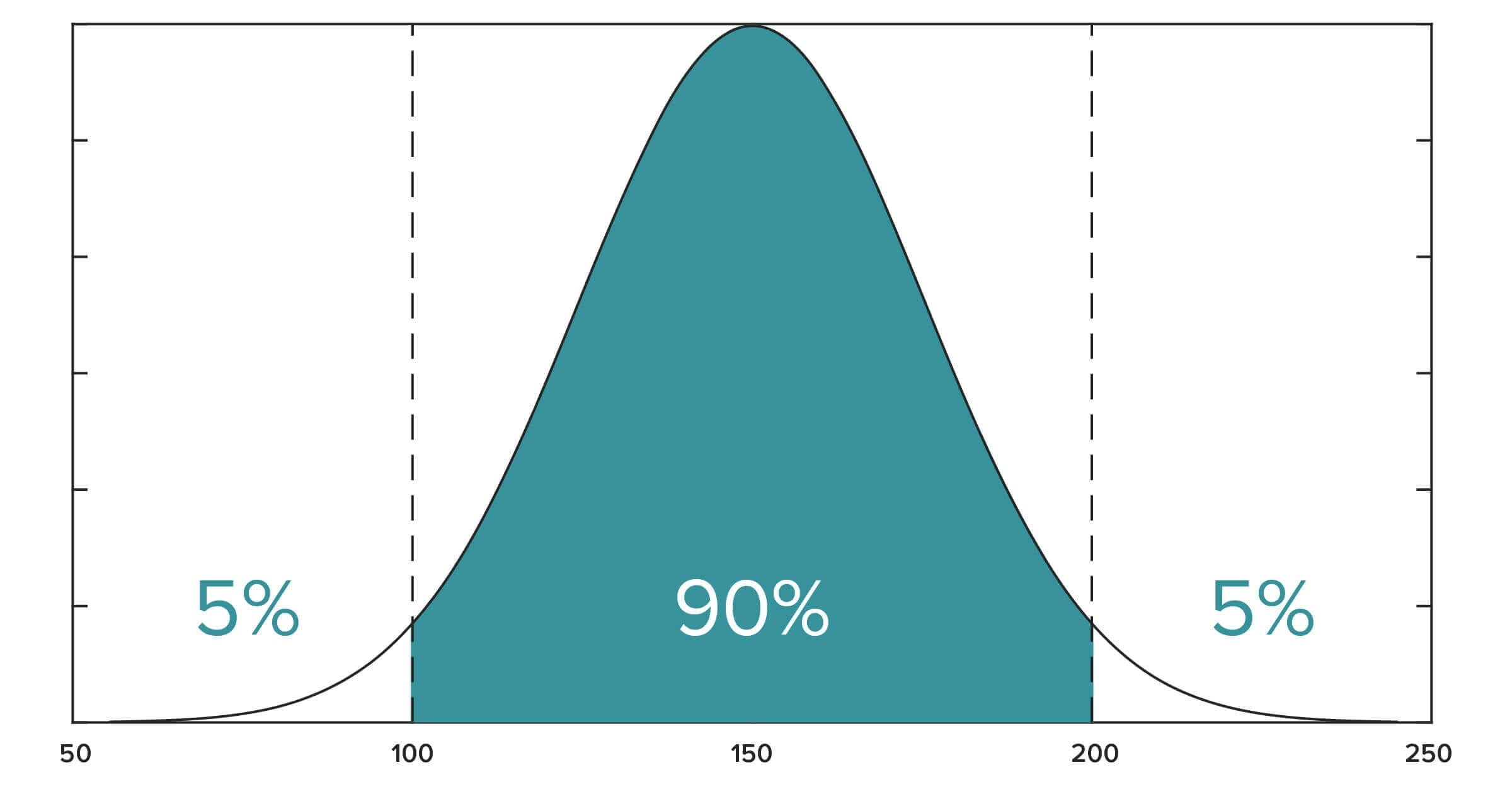
(123, 456) is a 95 confidence interval for. In order to have a meaningful statement, you need all three elements. Third there is the parameter being estimated, something like the population mean. Second is the confidence level, something like 95. The t α value for 24 with a confidence level of 95, we obtain the value of 2.064. Since the sample size is small (below 30), we take the sample size and subtract 1 to get the degrees of freedom (df). Step 2: Subtract the confidence level from 1, then divide by two. This gives you degrees of freedom, which you’ll need in step 3. Step 1: Subtract 1 from your sample size. The resultant confidence interval will be computed and displayed.Ĭalculating the confidence interval for a given group can be useful for any science, including electronics.Ĭalculate the 95% confidence interval for a data set given its mean cost is $193.73, its standard deviation is $26.73, and its sample size is 25. Find a confidence interval for a sample for the true mean weight of all foot surgery patients. What is the z-score for 99 confidence interval The z-score for a two-sided 99 confidence interval is 2.807, which is the 99.5-th quantile of the standard normal distribution N(0,1). To use this calculator, a user simply enters in the mean, standard deviation, the sample size of the data, and the confidence interval s/he wants toįind out, and clicks the 'Calculate' button. The z-score for a two-sided 95 confidence interval is 1.959, which is the 97.5-th quantile of the standard normal distribution N(0,1). Working in percentile form you have 100-95 which yields a value of 5, or 0.05 in decimal form. We calculate the lower estimate by the formula, lower estimate= mean - (standard deviation)(value of t α). OK, for a 95 confidence interval, you want to know how many standard deviations away from the mean your point estimate is (the 'z-score'). The value of t α is obtained by looking up the value based on a table. Once we obtain this value, we calculate the upper estimate of the interval by the formula, upper estimate= mean + (standard deviation)(value of t Sample size, according to the formula, σ x= σ/√n. The confidence interval calculator calculates the confidence interval by taking the standard deviation and dividing it by the square root of the The confidence interval of 99.9% will yield the largest range of all the confidence intervals. Which of the following values is within the 95 confidence interval (z-score 1. The confidence level, we get a larger and larger range. Remember, the margin of error, ME, can be determined using the formula, A simple random sample of 60 is drawn from a normally distributed population, and the mean is found to be 28, with a standard deviation of 5. This calculator calculates the upper and lower estimates for a given confidence interval based on the mean, sample size, and standard deviation values. The confidence level, we get a larger range of values to increase our confidence that the mean will be in the subset. This means that we are 95% confident that the mean is between 18.9 and 47.9.Ī confidence level of 50% will yield the shortest interval because it is the smallest and the least precise of all the confidence levels.

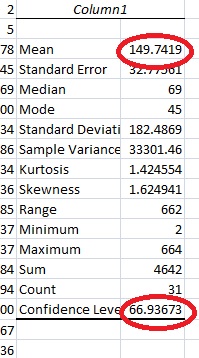
If we do so, we will get the interval of 18.9 to 47.9. We want to calculate the 95% confidence intervalįor this data. This calculator allows us to calculate the confidence interval for a group of data for 50%, 60%, 70%, 80%, 90%, 95%, 98%, 99%, 99.8%, and 99.9% confidenceįor example, let's say we have a sample size of 32, with a mean of 33.4 and a standard deviation of 42. The confidence interval allows us to quantify how confident we can feel a group of data is from its mean value. Standard deviation, and sample size for the data unit. This Confidence Interval Calculator calculates the confidence interval for group of data, given we have the mean,


 0 kommentar(er)
0 kommentar(er)
